:利用分数阶算法对经典LMS进行改进,并对发动机主动悬置系统的次级通道开展辨识,完成了不同分数阶次下的辨识试验,与经典LMS算法的辨识结果进行了对比,最后进行了振动主动控制试验。根据结果得出:在保证AEM系统振动主动控制效果的前提下,分数阶LMS相比于经典LMS具有更快的收敛速度,能改善算法的控制精度等优势。
随着发动机混动、变缸和主动启停等节能减排技术的蓬勃发展,传统的被动悬置难以应对日益复杂的发动机振动,而发动机主动悬置(Active Engine Mount,AEM)是解决这一问题的最佳方案[1]。主动悬置能够准确的通过发动机工况实时调节作动力以消减发动机振动,满足悬置动刚度和阻尼特性的隔振要求,慢慢的变成为近年来振动控制领域的研究热点之一[2]。为了更好的提高AEM的控制性能,学者们提出并探索了各种控制算法,FxLMS类算法因具备能够解决其在复杂多变环境下的高不确定性问题的能力在该领域被重点研究,而次级通道辨识结果的优劣对FxLMS算法的效果有着较大影响[3]。拓展的次级通道不仅应包括从输入电压到传递力的传递路径,还包括传感器、控制器在内的电子路径和传递力到加速度的机械路径[4]。Wang H 等[5]采用基于自适应陷波滤波器的频率来估计噪声信号频率改进的窄带有源噪声控制管理系统改善了时变系统的降噪性。俞翔等[6]提出了一种建模快速准确,降低计算量,提高了收敛速度和控制精度的变步长次级通道辨识算法。冷仓田等[7]采用神经网络对次级通道进行了辨识,并在管道有源噪声控制试验平台做噪声控制试验。刘昊等[8]采用反馈式次级通道阻尼补偿方法设计控制算法,仿真根据结果得出该方法具有收敛速度快和控制效果好、鲁棒性强等特点。袁军等[9]提出利用建模精度的变化来决定步长变化的2种方法,仿真根据结果得出所提出的方法有一定的效果。柯琦晖等[10]针对有源消声自动控制系统,提出了一种利用非参数模型估计方法来进行通道辨识的方式。高伟鹏[11]等针对主动控制系统中次级通道时变性强的问题,利用小波变换进行次级通道在线辨识,根据结果得出改进后辨识精度高,收敛速度快,控制效果好。
但是,不同的应用场景,针对不同的次级通道辨识对象,适合的次级通道辨识算法也不相同,因此成为了研究的难、重点[12]。目前仍缺乏针对汽车AEM 系统振动主动控制场景的次级通道辨识方法的针对性研究,而且辨识速度慢、资源占用大等问题仍制约着该技术的工程化。因此,在满足计算复杂度的前提下需尽可能快地提高其次级通道辨识的速度与准确性。本文提出将分数阶算法和经典LMS相结合应用于AEM 系统的次级通道辨识,在资源占用优化的情况下优化了辨识收敛速度。
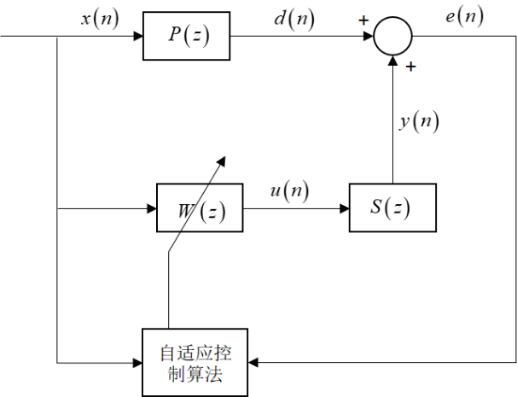

由式(3) 可知,控制器传递函数与次级通道传递函数紧密关联。目前,次级通道辨识激励手段一般有白噪声、线性正弦扫频和指数正弦扫频3 种,应用手段有离线辨识和在线]。本文采用白噪声激励的方式,则次级通道辨识过程示意图如图2 所示。
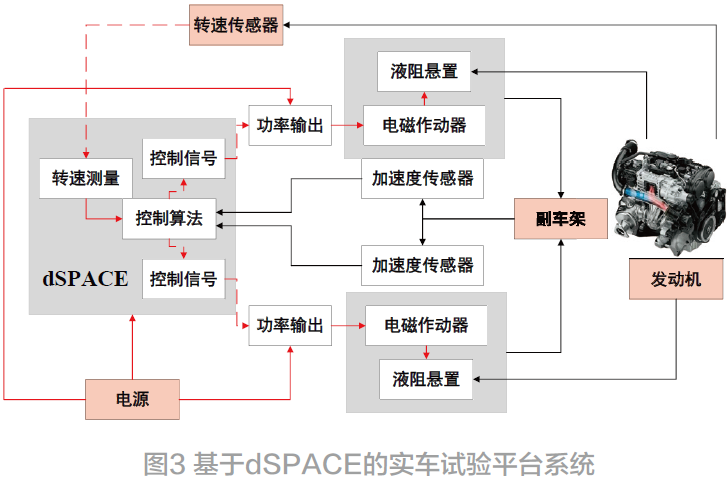
为评价两种次级通道辨识方法的性能,在AEM实车平台做试验。其中试验车动力源为直列四缸发动机,动力总成安装形式为纵置式,动力总成前端左、右各布置有一个主动悬置,其类型为液压复合解耦盘+电磁作动器式。后方变速箱居中位置布置了两个橡胶悬置,其位置紧密相接,可简化为1 个前悬置,呈3 点式悬置结构
分数阶LMS 和经典LMS 辨识次级通道。在振动主动控制的实际应用中,评价指标主要包括收敛性能和稳态失调性能,其中收敛速度表征了非稳态环境下算法准确跟踪权系数变化的能力,而稳态失调性能表征了权系数收敛到最优值时仍存在的最小均方误差。两种算法的步长取值均为10-5,滤波器长度为128 阶,其中分数阶LMS 算法阶次分别取0.1、0.3、0.5、0.7、0.9。
图4 为经典LMS 和不同阶次的分数阶LMS 性能对比图,可见当迭代次数足够时,不同阶次的分数阶LMS 与经典LMS 的稳态失调量几乎一致。当分数阶阶次较低时,其收敛速度和稳态失调量与经典LMS 几乎相同,而当分数阶LMS 算法阶次提高时,其稳态失调量能在较小的迭代次数时达到收敛。以均方误差作为收敛速度的判断指标,可知随着算法阶次的提高,分数阶LMS的收敛速度逐渐变大,当分数阶LMS阶次为0.5 时,收敛速度与经典LMS 相近;当阶次低于0.5 时,收敛速度低于LMS 算法;而当阶次高于0.5 时,收敛速度将高于LMS 算法。
进一步分析两种方法的次级通道幅频特性曲线所示,两种方法求得的幅频特性曲线几乎一致,其中幅值衰减较大,最大达到75 dB 左右,相位差最大约50°。只要辨识次级通道与实际次级通道相位差 90°系统控制就是可以收敛的[17]。

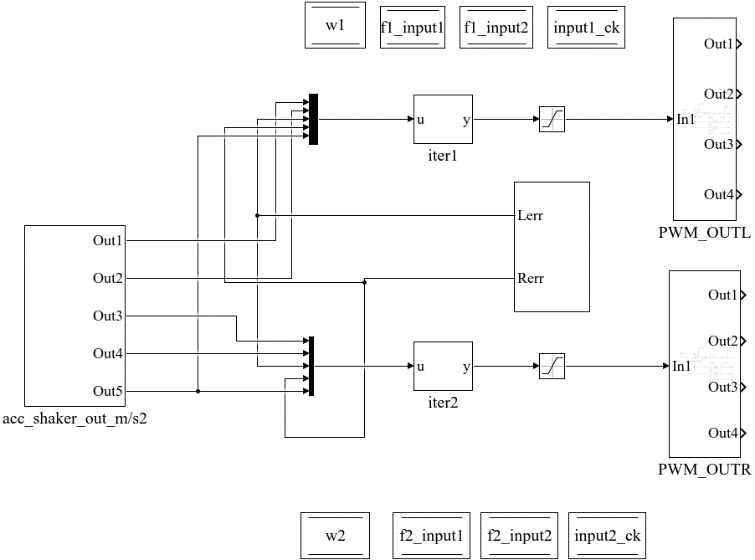
发动机主动悬置控制系统的快速控制原型。为观察次级通道辨识效果在所关注频段对发动机主动悬置控制系统控制效果的影响,在定置上升工况下做试验,试验过程中发动机转速由怠速缓慢、均匀地上升至4 200 r/min,测量无控制情况及应用不同算法的次级通道辨识结果时的误差传感器信号,并在时域和频域下分别作对比验证。
;经典LMS 次级通道辨识模型下左测点误差传感器处的全程加速度均方根值为0.040 1 m/s,相比于无控制情况下下降了64.70%,右测点误差传感器处的全程加速度均方根值为0.021 8 m/s,相比于无控制情况下下降了46.70%;在0.9 分数阶次级通道辨识模型下左测点误差传感器处的全程加速度均方根值为0.041 6 m/s,相比于无控制情况下降了63.38%,右测点误差传感器处的全程加速度均方根值为0.020 3 m/s
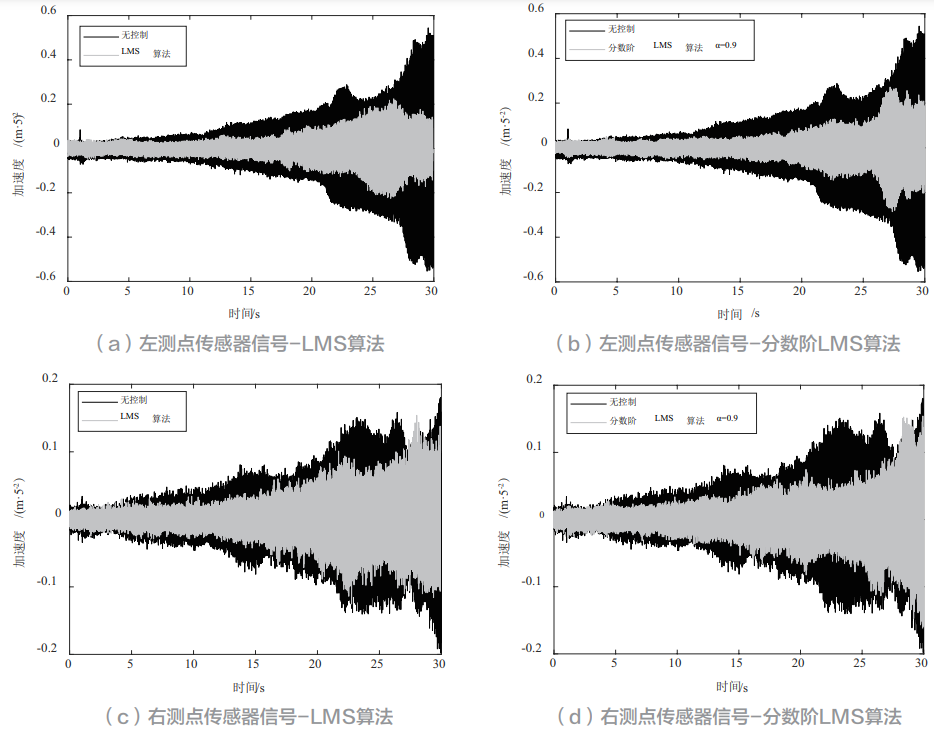
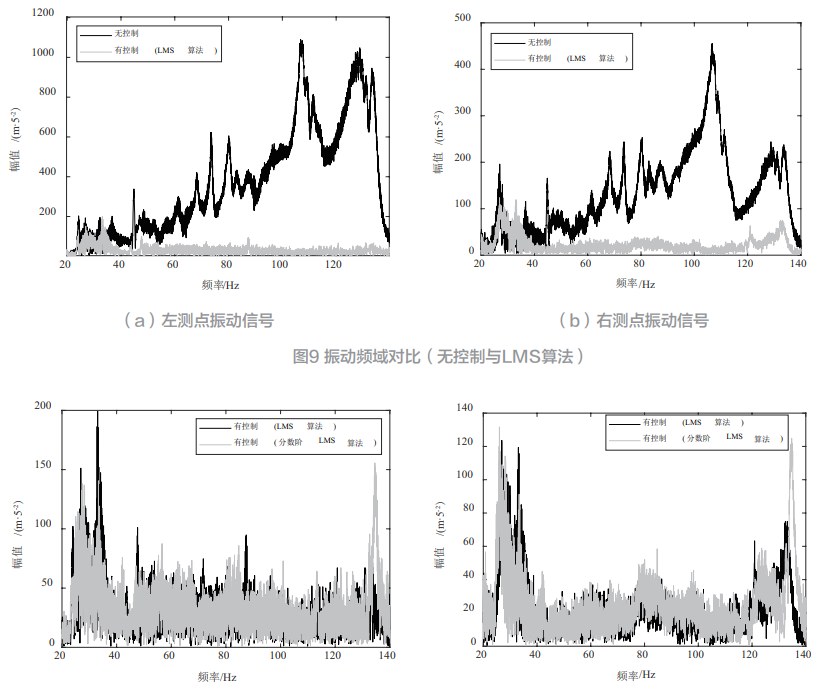
对时域信号进行傅里叶变换,无控制情况与应用经典LMS 次级通道辨识模型下系统振动结果频域对比如图9 所示,可见有控制情况下对振动有着非常明显的压制效果。应用经典LMS 与应用分数阶LMS 次级通道辨识模型的系统振动结果频域对比图如图10 所示,由图10 可知二者对所关注频段内振动抑制效果几乎一致,即分数阶LMS 次级通道辨识算法在保证振动抑制效果的情况下具有更快的辨识速度。
本文针对汽车AEM 系统中的次级通道辨识问题,提出了分数阶LMS 辨识算法。仿真分析了在不同算法阶次条件下的算法性能。最后将分数阶LMS 方法的辨识结果用于汽车AEM 系统开展振动主动控制试验,并与经典LMS 作对比。结果显示:随着算法阶次的增加,收敛速度得到稳步提高,当算法阶次高于0.5 时,收敛速度相比于LMS 算法有明显提升,稳态失调量也
能保持恒定。将0.9 分数阶时的次级通道辨识结果应用于AEM 系统来进行对比试验,结果显示两种算法的减振效果几乎相同,说明分数阶LMS 次级通道辨识算法在提升辨识速度的同时保证了AEM 系统的振动主动抑制效果。


